Mengenal Koordinat Kartesius Dan Polar Dalam Matematika

Mengenal Koordinat Kartesius dan Polar dalam Matematika - Dalam ilmu Matematika niscaya kita sudah tidak ajaib lagi dengan istilah koordinat kartesius Matematika. Sistem koordinat ini dipakai untuk memilih letak titik relatif yang terdapat diantara dua sumbu, yakni sumbu x dan y. Penulisan koordinat dalam kartesius sanggup berupa (x, y), dimana x yakni absis yang letak posisi titik relatifnya di sumbu x dan y yakni ordinat yang letak posisi titik relatifnya di sumbu y. Koordinat Matematika tidak hanya kartesius saja, tetapi juga koordinat polar. Namun kedua jenis koordinat ini berbeda satu sama lain. Biasanya kartesius dipakai untuk menuntaskan perhitungan geometri dan aljabar dalam Matematika.

Polar merupakan salah satu jenis koordinat Matematika. Jenis koordinat ini sanggup dinamakan dengan koordinat kutub. Polar dipakai untuk menggambarkan letak titik sesuai dengan jarak menuju titik pusatnya dan sudut di sumbu x. Polar dengan kartesius mempunyai hubungan yang sangat erat. Maka dari itu koordinat dalam kartesius sanggup dikonversikan menjadi polar, begitu pula sebaliknya. Nah dalam pembahasan kali ini saya akan menjelaskan perihal koordinat kartesius dan koordinat polar dalam Matematika. Untuk lebih jelasnya sanggup anda simak di bawah  ini.

Mengenal Koordinat Kartesius dan Polar dalam Matematika

Sudah saya jelaskan di atas bahwa koordinat kartesius dan koordinat polar saling bekerjasama satu sama lain. Untuk itu kedua jenis koordinat tersebut sanggup dikonversikan satu sama lain. Agar anda lebih memahami mengenai kedua koordinat Matematika ini, maka sanggup anda perhatikan gambar berikut:

Baca juga : Cara Menggambar Diagram Venn Beserta Contohnya

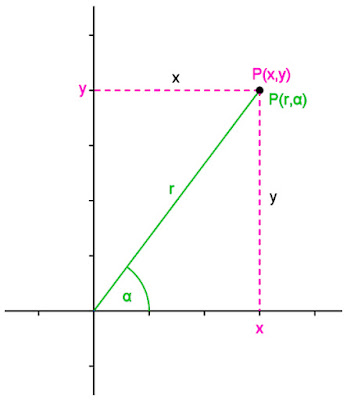Ilustrasi Koordinat Kartesius dengan Koordinat Polar

Berdasarkan gambar diatas, kita sanggup memilih dua koordinat melalui posisi P yaitu koordinat kartesius (dilambangkan dengan x, y) beserta koordinat polar (dilambangkan dengan r, α). Kartesius dalam koordinat x, y menggambarkan letak titik relatif di sumbu x dan y. Kemudian polar dalam koordinat r menggambarkan jarak antara sebuah titik dengan titik sentra O dan sudut α menggambarkan hasil pembentukan sudut antara sumbu x positif dengan ruas garis OP. Lantas bagaimana kedua koordinat Matematika tersebut sanggup dihubungkan? Bagaimana cara mengkonversikan kartesius menjadi polar dan begitu pula sebaliknya?

Hubungan Koordinat Kartesius dengan Koordinat Polar (Kutub)

Hubungan antara koordinat kartesius dan koordinat polar ditunjukan dengan jarak titik asal O (0,0) dengan titik P (x, y). Jarak tersebut sanggup dinamakan dengan jarak r. Untuk memperoleh nilai r tersebut sanggup memakai rumus di bawah ini:

Rumus Jarak r

Kemudian koordinat kartesius dan koordinat polar akan menghasilkan sebuah sudut α. Sudut α ialah sudut yang terletak diantara garis hubung P terhadap titik O (0,0) dengan sumbu X positif. Namun perhitungannya berlawanan arah dengan arah pada jarum jam. Titik P tersebut sanggup dinyatakan dalam bentuk koordinat kutub yaitu P (r, α).

Koordinat kartesius dengan koordinat polar sanggup digambar menjadi grafik ibarat di bawah ini:

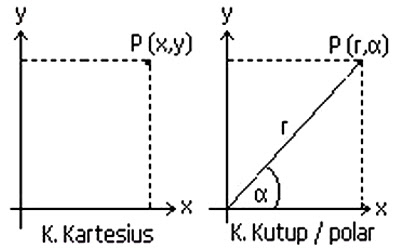Grafik Kartesius dan Polar

Titik sentra pada koordinat kutub mempunyai letak titik P yang sanggup digambarkan dengan (r, α). r menerangkan jarak OP, sedangkan α menerangkan sudut antara sumbu OX positif dengan OP. Untuk itu perhitungan besar sudut α berawal dari sumbu OX positif dan berputar berkebalikan dengan arah jarum jam.

Baca juga : Materi Grafik Fungsi Trigonometri (Sin, Cos, Tan) Lengkap

Persamaan dan Perbedaan Koordinat Kartesius Dengan Koordinat Polar

Persamaan antara kartesius dengan polar ialah sama sama termasuk koordinat Matematika. Namun jikalau ditinjau dari segi perbedaannya, maka sanggup anda perhatikan klarifikasi masing masing koordinat yaitu meliputi:

Koordinat Kartesius
Peletakkan titik P pada kartesius sanggup ditunjukan dalam bentuk himpunan pasangan berurutan yakni P (x, y), dimana :

• Koordinat x disebut absis, yakni jarak antara titik menuju sumbu Y.
• Koordinat y disebut ordinat, yakni jarak antara titik menuju sumbu X.

Koordinat Polar (Kutub)
Letak P pada koordinat kutub sanggup digambarkan dalam bentuk ukuran jarak r dengan sudut α. Dimana:

• Jarak r ialah jarak anatara titik P (x, y) menuju titik asal O (0,0). Untuk memperoleh besar jarak r sanggup memakai rumus pythagoras yakni r² = x² + y².
• Titik P pada koordinat kutub sanggup digambarkan dalam bentuk P (r, α).
• Sudut α ialah sudut yang dibuat antara garis hubung pada titik P terkadap titik O (0,0) dengan sumbu X positif, dimana peritungan arahnya berkebalikan dengan arah jarum jam.

Mengubah Koordinat Kartesius Menjadi Koordinat Polar

Dalam mengubah koordinat kartesius menjadi koordinat polar sanggup dilakukan dengan menciptakan sebuah grafik yang menghubungkan kedua koordinat Matematika tersebut. Jika keduanya digabungkan dalam satu koordinat, maka akan membentuk sebuah segitiga siku siku dimana panjang sisinya berupa sisi x, y dan r. Untuk memperoleh jarak r sanggup memakai konsep teorema pythagoras yakni:

Rumus Jarak r

Selain menerapkan konsep teorema pythagoras, tetapi juga menerapkan perbandngan trigonometri ibarat di bawah ini:

Konsep Perbandingan Trigonometri

Kesimpulan:

Untuk mengubah koordinat kartesius (x, y) menjadi koordinat polar (r, α), maka memakai hukum ibarat di bawah ini:

Rumus Konversi Koordinat Kartesius Menjadi Koordinat Polar

Mengubah Koordinat Polar Menjadi Koordinat Kartesius

Dalam mengubah koordinat polar menjadi koordinat kartesius sanggup dilakukan dengan menciptakan sebuah grafik yang menghubungkan kedua koordinat Matematika tersebut. Jika keduanya digabungkan dalam satu koordinat, maka akan membentuk sebuah segitiga siku siku dimana panjang sisinya berupa sisi x, y dan r.  Dalam mengubah koordinat kutub menjadi kartesius intinya memakai konsep perbandingan trigonometri ibarat di bawah ini:

Baca juga : Rumus Persamaan Garis Singgung Lingkaran Beserta Contoh Soal

Konsep Perbandingan Trigonometri

Kesimpulan:

Untuk mengubah koordinat polar (r, α) menjadi koordinat kartesius (x, y), maka memakai hukum ibarat di bawah ini:

Rumus Konversi Koordinat Polar Menjadi Koordinat Kartesius

Contoh Soal

1. Ubahlah koordinat kartesius (1, 1) menjadi koordinat polar?

Jawab.

Jawaban Contoh Soal 1

Makara koordinat polarnya ialah (r, α) = (√2, 45°).

2. Konversikan koordinat polar (2 30°) menjadi koordinat kartesius?

Jawab.

Jawaban Contoh Soal 2

Makara koordinat kartesiusnya ialah (x, y) = (√3, 1)

Sekian klarifikasi mengenai koordinat kartesius dan koordinat polar dalam Matematika. Kedua koordinat Matematika tersebut dapar dihubungkan satu sama lain dalam sebuah grafik. Semoga artikel ini sanggup bermanfaat dan selamat belajar.